Ο ক)
|
যৌগিক রাশি
|
Ο খ)
|
ভেক্টর রাশি
|
Ο গ)
|
ভেক্টর রাশি
|
Ο ঘ)
|
মৌলিক রাশি
|
সঠিক উত্তর:
(খ)
২.
|
কোনো ত্রিভুজের শীর্ষত্রয়ের অবস্থান ভেক্টর যথাক্রমে a, b ও c হলে, তাদের মধ্যমা তিনটির ছেদ বিন্দুর অবস্থান ভেক্টর কী হবে? |
Ο ক)
|
1/3(a + b + c)
|
Ο খ)
|
1
|
Ο গ)
|
2
|
Ο ঘ)
|
3
|
সঠিক উত্তর:
(ক)
৩.
|
সামান্তরিক বিধি প্রযোজ্য হয় না দুইটি ভেক্টরের কোন সম্পর্কের ক্ষেত্রে? |
Ο ক)
|
দিক সমান
|
Ο খ)
|
সমান্তরাল
|
Ο গ)
|
বিপরীতমুখী
|
Ο ঘ)
|
মান সমান
|
সঠিক উত্তর:
(খ)
৪.
|
ভেক্টর পদ্ধতিগতভাবে প্রথম প্রচলন শুরু করেন কোন বিজ্ঞানী? |
Ο ক)
|
রোওয়ান হ্যামিলটন
|
Ο খ)
|
নিউটন
|
Ο গ)
|
গিবস
|
Ο ঘ)
|
এরিস্টোটল
|
সঠিক উত্তর:
(ক)
৫.
|
দিক নির্ভরতা অনুসারে রাশিকে কয়ভাগে ভাগ করা যায়? |
Ο ক)
|
পাঁচ
|
Ο খ)
|
তিন
|
Ο গ)
|
দুিই
|
Ο ঘ)
|
চার
|
সঠিক উত্তর:
(গ)
৬.
|
ABCD সামান্তরিকের AC এভং BD কর্ণদ্বয়ের ছেদবিন্দু O. তাহলে নিম্নের কোনটি সঠিক? |
Ο ক)
|
AO = OC এবং BO = OD
|
Ο খ)
|
AO = OD এবং BO = OC
|
Ο গ)
|
AO = OB এবং CO = 0D
|
Ο ঘ)
|
AD = BO
|
সঠিক উত্তর:
(ক)
Ο ক)
|
স্কেলার রাশি
|
Ο খ)
|
ভেক্টর রাশি
|
Ο গ)
|
লব্ধ রাশি
|
Ο ঘ)
|
মৌলিক রাশি
|
সঠিক উত্তর:
(খ)
৮.
|
u, y ভেক্টরের জন্য u + v = v +u প্রকাশ করে
i. যোজন বিধি
ii.� বিয়োজন বিধি
iii. গুণন বিধি
নিচের কোনটি সঠিক? |
Ο ক)
|
শুধু i
|
Ο খ)
|
শুধু ii
|
Ο গ)
|
iii
|
Ο ঘ)
|
i, ii ও iii
|
সঠিক উত্তর:
(ক)
৯.
|
2 টাকা, 3 cm, 5 ইত্যাদি কোন জাতীয় রাশি? |
Ο ক)
|
একক রাশি
|
Ο খ)
|
যৌগিক রাশি
|
Ο গ)
|
স্কেলার রাশি
|
Ο ঘ)
|
মৌলিক রাশি
|
সঠিক উত্তর:
(গ)
১০.
|
m ও n ধনাত্মক হলে, (m + n)u ভেক্টরটির মান কত হয়? |
Ο ক)
|
m + n
|
Ο খ)
|
mn |u|
|
Ο গ)
|
|m + n||u|
|
Ο ঘ)
|
|m + n|u
|
সঠিক উত্তর:
(গ)
১১.
|
m, n দুইটি স্কেলার রাশি এবং u, v দুইটি ভেক্টর হলে নিচের কোনটি ভেক্টরের বন্টনসূত্র অনুসরণ করে? |
Ο ক)
|
(m + n)u = mu + nu
|
Ο খ)
|
m+nu
|
Ο গ)
|
m(u + v)
|
Ο ঘ)
|
(u + v)m = mu + mv
|
সঠিক উত্তর:
(ক)
Ο ক)
|
স্কেলার রাশি
|
Ο খ)
|
ভেক্টর রাশি
|
Ο গ)
|
লব্ধ রাশি
|
Ο ঘ)
|
মৌলিক রাশি
|
সঠিক উত্তর:
(ক)
১৩.
|
m, n দুইটি ঋণাত্মক স্কেলার ও u একটি ভেক্টর হলে-
i. (m + n)u এর মান |m + n| |u|.
ii. (m + n)u এর দিক হবে, u এর বিপরীত দিকে।
iii. (m + n)u এর দৈর্ঘ্য হবে 0.
নিচের কোনটি সঠিক? |
Ο ক)
|
i ও ii
|
Ο খ)
|
i
|
Ο গ)
|
ii
|
Ο ঘ)
|
iii
|
সঠিক উত্তর:
(ক)
১৪.
|
m ও n উভয়ই ঋণাত্মক হলে, (m + n) v ও v ভেক্টরের দিকের সম্পর্ক কী? |
Ο ক)
|
পরস্পর লম্ব
|
Ο খ)
|
বিপরীত
|
Ο গ)
|
একই দিক
|
Ο ঘ)
|
সমান্তরাল ও একই দিক
|
সঠিক উত্তর:
(খ)
১৫.
|
u, v, w এর জন্য (u + v ) + w = u + (v + w) প্রকাশ করে
i. যোজন বিধি
ii. বিয়োজন বিধি
iii. সহ যোজন বিধি
নিচের কোনটি সঠিক? |
Ο ক)
|
i
|
Ο খ)
|
ii
|
Ο গ)
|
i ও iii
|
Ο ঘ)
|
iii
|
সঠিক উত্তর:
(গ)
১৬.
|
সমজাতীয় এবং সমমানের দুইটি ভেক্টরের দিক যদি পরস্পর বিপরীতমুখী হয় তাহলে এদের একটিকে অপরটির কোন ভেক্টর বলে? |
Ο ক)
|
বিপরীত
|
Ο খ)
|
শূন্য ভেক্টর
|
Ο গ)
|
সমান
|
Ο ঘ)
|
অবস্থান
|
সঠিক উত্তর:
(ক)
১৭.
|
স্কেলার রাশির উদাহরণ-
i. দৈর্ঘ্য ও ভর।
ii. দ্রুতি ও সময়।
iii. আয়তন ও তাপমাত্রা।
নিচের কোনটি সঠিক? |
Ο ক)
|
i
|
Ο খ)
|
ii
|
Ο গ)
|
iii
|
Ο ঘ)
|
i, ii ও iii
|
সঠিক উত্তর:
(ঘ)
১৮.
|
নিচের রাশিগুলোর মধ্যে কোনটি স্কেলার রাশি? |
Ο ক)
|
বেগ
|
Ο খ)
|
সরণ
|
Ο গ)
|
তাপমাত্রা
|
Ο ঘ)
|
তড়িৎ প্লাবল্য
|
সঠিক উত্তর:
(গ)
১৯.
|
u এর বিপরীত ভেক্টর v হবে যদি-
i. |v| = |u|
ii. v এর ধারক রেখা u এর ধারক রেখার সঙ্গে অভিন্ন বা সমান্তরাল হয়
iii. u এর দিক v এর দিকের বিপরীত হয়
নিচের কোনটি সঠিক? |
Ο ক)
|
i
|
Ο খ)
|
ii
|
Ο গ)
|
iii
|
Ο ঘ)
|
i, ii ও iii
|
সঠিক উত্তর:
(ঘ)
২০.
|
কোনো ভেক্টর মুলবিন্দুর সাপেক্ষে D, E ও F বিন্দুর অবস্থান ভেক্টর যথাক্রমে a, b ও c । F বিন্দুতে DE রেখাংশ 7 : 3 অনুপাতে বহির্বিভক্ত হলে, c = কত? |
Ο ক)
|
7b - 3a/4
|
Ο খ)
|
3a - 7b
|
Ο গ)
|
0
|
Ο ঘ)
|
1
|
সঠিক উত্তর:
(ক)
২১.
|
নিচের কোনটি স্কেলার রাশি? |
Ο ক)
|
সরণ
|
Ο খ)
|
ত্বরণ
|
Ο গ)
|
দৈর্ঘ্য
|
Ο ঘ)
|
ওজন
|
সঠিক উত্তর:
(গ)
২২.
|
নিচের কোনটি ভেক্টর রাশি? |
Ο ক)
|
আয়তন
|
Ο খ)
|
দৈর্ঘ্য
|
Ο গ)
|
সময়
|
Ο ঘ)
|
সরণ
|
সঠিক উত্তর:
(ঘ)
২৩.
|
u, v এবং u + v দ্বারা ত্রিভুজ উৎপন্ন করা সম্ভব যখন-
i. u এর আদিবিন্দু, v এর প্রান্ত বিন্দু যোগ করা যাবে।
ii. u + v এর আদি বিন্দু ও অন্তবিন্দু যথাক্রমে v এর আদিবিন্দু এবং u এর প্রান্তবিন্দু হবে।
iii. u ও v সমান্তরাল।
নিচের কোনটি সঠিক? |
Ο ক)
|
i ও ii
|
Ο খ)
|
i
|
Ο গ)
|
ii
|
Ο ঘ)
|
iii
|
সঠিক উত্তর:
(ক)
২৪.
|
স্কেলার রাশির-
i. কেবলমাত্র মান আছে।
ii. কেবলমাত্র দিক আছে।
iii. মান আছে কিন্তু দিক নাই।
নিচের কোনটি সঠিক? |
Ο ক)
|
i
|
Ο খ)
|
i ও iii
|
Ο গ)
|
ii
|
Ο ঘ)
|
iii
|
সঠিক উত্তর:
(খ)
২৫.
|
u = v এবং� v = w সম্পর্ক দুটি দ্বারা কোন সম্পর্কটি তৈরি করা যায়? |
Ο ক)
|
v = - u
|
Ο খ)
|
w = -v
|
Ο গ)
|
u = v + w
|
Ο ঘ)
|
u = w
|
সঠিক উত্তর:
(ঘ)
|
২৬.
|
“বাঁশটি ৫ মিটার লম্বা”- কথাটিতে কোন রাশির প্রকাশ হয়েছে? |
Ο ক)
|
স্কেলার
|
Ο খ)
|
সদিক
|
Ο গ)
|
ভেক্টর
|
Ο ঘ)
|
দিক
|
সঠিক উত্তর:
(ক)
২৭.
|
পদার্থের আকর্ষণ ও বিকর্ষন কোন ধরনের রাশি? |
Ο ক)
|
ভেক্টর
|
Ο খ)
|
স্কেলার
|
Ο গ)
|
মৌলিক
|
Ο ঘ)
|
যৌগিক
|
সঠিক উত্তর:
(ক)
২৮.
|
যে সকল রাশিকে কেবলমাত্র এককসহ পরিমাণ দ্বারা সম্পূর্ণরূপে বোঝানো যায় ঐ রাশির নাম কি? |
Ο ক)
|
নির্দিক
|
Ο খ)
|
দিক
|
Ο গ)
|
ভেক্টর
|
Ο ঘ)
|
সদিক
|
সঠিক উত্তর:
(ক)
২৯.
|
দুইটি ভেক্টর পরস্পর সমান এবং তাদের দৈর্ঘ্য সমান, ধারক রেখা একই বা সমান্তরাল এবং দিক একই তবে, তাকে কী বলে? |
Ο ক)
|
সমান্তরাল ভেক্টর
|
Ο খ)
|
সমান ভেক্টর
|
Ο গ)
|
সদৃশ ভেক্টর
|
Ο ঘ)
|
একক ভেক্টর
|
সঠিক উত্তর:
(খ)
৩০.
|
AEFB চতুর্ভুজ ভেক্টর যোগের কোন বিধি মেনে চলে? |
Ο ক)
|
ত্রিভুজবিধি
|
Ο খ)
|
রম্বসবিধি
|
Ο গ)
|
সামান্তরিকবিধি
|
Ο ঘ)
|
বর্গবিধি
|
সঠিক উত্তর:
(গ)
Ο ক)
|
সেকেন্ড
|
Ο খ)
|
মিটার
|
Ο গ)
|
ঘন্টা
|
Ο ঘ)
|
মিটার/সেকেন্ড
|
সঠিক উত্তর:
(ঘ)
৩২.
|
কোন রেখাংশের এক প্রান্তকে কী বলে? |
Ο ক)
|
আদি বিন্দু
|
Ο খ)
|
প্রান্তবিন্দু
|
Ο গ)
|
অন্তবিন্দু
|
Ο ঘ)
|
নির্দেশক
|
সঠিক উত্তর:
(ক)
৩৩.
|
m, n দুইটি স্কেলার এবং u, v দুইটি ভেক্টর হলে, নিচের কোনটি ভেক্টরের বন্টন সূত্র অনুসরণ করে? |
Ο ক)
|
(m + n) u = mu + nu
|
Ο খ)
|
(m + n) u
|
Ο গ)
|
m(u + v)
|
Ο ঘ)
|
(u + v)m
|
সঠিক উত্তর:
(ক)
৩৪.
|
একটি ভেক্টর u অপর একটি ভেক্টর v এর সমান হলে-
i. u এর দৈর্ঘ্য সমান v এর দৈর্ঘ্য।
ii. u এবং v সমান্তরাল ভেক্টর।
iii. u এর দিক v এর দিকের সঙ্গে একমুখী।
নিচের কোনটি সঠিক? |
Ο ক)
|
i
|
Ο খ)
|
ii
|
Ο গ)
|
iii
|
Ο ঘ)
|
i, ii ও iii
|
সঠিক উত্তর:
(ঘ)
৩৫.
|
তিনটি ভেক্টর কীরূপ হলে ত্রিভুজ উৎপন্ন করা সম্ভব? |
Ο ক)
|
সমান্তরাল
|
Ο খ)
|
অসমান্তরাল
|
Ο গ)
|
মান একই
|
Ο ঘ)
|
ধারক একই
|
সঠিক উত্তর:
(খ)
৩৬.
|
কোনো ভেক্টর যে অসীম সরলরেখার অংশ সেটি কী রেখা? |
Ο ক)
|
ধারক
|
Ο খ)
|
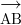
|
Ο গ)
|
সরলরেখা
|
Ο ঘ)
|
বক্ররেখা
|
সঠিক উত্তর:
(ক)
৩৭.
|
v এর অন্তবিন্দু, w এর আদিবিন্দু হলে, ভেক্টরদ্বয় কি হলে ত্রিভুজ উৎপন্ন করা সম্ভব? |
Ο ক)
|
সমান্তরাল
|
Ο খ)
|
অসমান্তরাল
|
Ο গ)
|
মান একই
|
Ο ঘ)
|
ধারক একই
|
সঠিক উত্তর:
(খ)
Ο ক)
|
0
|
Ο খ)
|
1
|
Ο গ)
|
|u|
|
Ο ঘ)
|
u
|
সঠিক উত্তর:
(ক)
৩৯.
|
ভেক্টর রাশির অপর নাম কী? |
Ο ক)
|
অদিক রাশি
|
Ο খ)
|
নির্দিক রাশি
|
Ο গ)
|
সদিক রাশি
|
Ο ঘ)
|
স্কেলার রাশি
|
সঠিক উত্তর:
(গ)
৪০.
|
নিচের কোনটি অদিক রাশি? |
Ο ক)
|
আয়তন
|
Ο খ)
|
বল
|
Ο গ)
|
ওজন
|
Ο ঘ)
|
সরণ
|
সঠিক উত্তর:
(ক)
৪১.
|
p ধনাত্মক ও q ঋণাত্মক স্কেলার হলে (p + q)v ভেক্টরটির মান কত? |
Ο ক)
|
|p + q| |v|
|
Ο খ)
|
1
|
Ο গ)
|
2
|
Ο ঘ)
|
3
|
সঠিক উত্তর:
(ক)
৪২.
|
কোন ভেক্টর যে অসীম সরল রেখার অংশ বিশেষ তাকে ঐ ভেক্টরের কী বলা হয়? |
Ο ক)
|
ধারক রেখা
|
Ο খ)
|
আদিরেখা
|
Ο গ)
|
শুধু ধারক
|
Ο ঘ)
|
ক ও গ
|
সঠিক উত্তর:
(ঘ)
৪৩.
|
শূন্য ভেক্টরের-
i. দিক নির্ণয় করা যায়
ii. পরমান শূন্য
iii. ধারক রেখা নেই
নিচের কোনটি সঠিক? |
Ο ক)
|
i
|
Ο খ)
|
ii
|
Ο গ)
|
ii ও iii
|
Ο ঘ)
|
iii
|
সঠিক উত্তর:
(গ)
৪৪.
|
দুইটি ভেক্টর সমান্তরাল হলে-
i. এদের যোগের ক্ষেত্রে সামান্তরিক বিধি প্রযোজ্য
ii. এদের যোগের ক্ষেত্রে ত্রিভুজ বিধি প্রযোজ্য
iii. এদের দৈর্ঘ্য সর্বদা সমান
নিচের কোনটি সঠিক? |
Ο ক)
|
i
|
Ο খ)
|
ii
|
Ο গ)
|
iii
|
Ο ঘ)
|
i, ii ও iii
|
সঠিক উত্তর:
(খ)
৪৫.
|
u একটি ভেক্টর, m ∈ R হলে, mu এর দিক u এর দিকে হবে যদি- |
Ο ক)
|
m < 0
|
Ο খ)
|
m > 0
|
Ο গ)
|
m = 0
|
Ο ঘ)
|
m ≠ 0
|
সঠিক উত্তর:
(খ)
Ο ক)
|
ভেক্টর
|
Ο খ)
|
স্কেলার
|
Ο গ)
|
মৌলিক
|
Ο ঘ)
|
যৌগিক
|
সঠিক উত্তর:
(খ)
৪৭.
|
যে রাশিকে পূর্ণরূপে প্রকাশ করার জন্য তার পরিমাণ ও দিক উভয়ের প্রয়োজন হয় তাকে কি রাশি বলা হয়? |
Ο ক)
|
ধারক রাশি
|
Ο খ)
|
অদিক রাশি
|
Ο গ)
|
স্কেলার রাশি
|
Ο ঘ)
|
ভেক্টর রাশি
|
সঠিক উত্তর:
(ঘ)
৪৮.
|
a + 5b = 0 হলে a ও� b ভেক্টরদ্বয় কীরূপ? |
Ο ক)
|
লম্ব
|
Ο খ)
|
সমান
|
Ο গ)
|
সমান্তরাল ও দিক একই
|
Ο ঘ)
|
সমান্তরাল ও বিপরীতমুখী
|
সঠিক উত্তর:
(ঘ)
উদ্দীপকটি পড় এবং নিচের দুইটি প্রশ্নের উত্তর দাও:
A, B ও C বিন্দুর অবস্থান ভেক্টর যথাক্রমে a, b ও c |
৪৯.
|
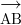 = কত? = কত? |
Ο ক)
|
b - a
|
Ο খ)
|
a + b
|
Ο গ)
|
b + a
|
Ο ঘ)
|
1/2(b - a)
|
সঠিক উত্তর:
(ক)
৫০.
|
যদি C বিন্দু AB এর মধ্যবিন্দু হয়, তাহলে- |
Ο ক)
|
(a - b)
|
Ο খ)
|
(b -a)
|
Ο গ)
|
c = 1/2(a + b)
|
Ο ঘ)
|
c = (a + b)
|
সঠিক উত্তর:
(গ) |
কোন মন্তব্য নেই:
একটি মন্তব্য পোস্ট করুন